Математическое моделирование сложных технологических процессов доменного производства методами нелинейной динамики тема диссертации и автореферата по ВАК РФ 05.13.18, кандидат технических наук Голубев, Олег Викторович

Содержание

Проблемы построения системы поддержки принятия решений для доменного производства Текст научной статьи по специальности «Математика»

В статье рассматривается возможность построения системы поддержки принятия решений для доменного производства. Приведен обзор моделей доменной печи . Рассмотрены параметры, которые должны быть представлены в проектируемой системе в качестве входных и выходных, проанализированы способы получения результатов (рекомендаций), представление их в удобной для пользователя форме

PROBLEMS OF CONSTRUCTING A DECISION SUPPORT SYSTEM FOR BLAST FURNACE

The possibility of constructing a decision support system for blast furnace production is considered in article. The review of models of blast furnace is presented. Parameters that must be submitted to the projected system as input and output are considered, ways of receipt of results, their representation in a user-friendly way are analyzed

Текст научной работы на тему «Проблемы построения системы поддержки принятия решений для доменного производства»

ПРОБЛЕМЫ ПОСТРОЕНИЯ СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ

ДЛЯ ДОМЕННОГО ПРОИЗВОДСТВА

В статье рассматривается возможность построения системы поддержки принятия решений для доменного производства. Приведен обзор моделей доменной печи. Рассмотрены параметры, которые должны быть представлены в проектируемой системе в качестве входных и выходных, проанализированы способы получения результатов (рекомендаций), представление их в удобной для пользователя форме

Ключевые слова: система поддержки принятия решений, доменная печь, математическая модель

В последние десятилетия происходит интенсификация технологических процессов в энергетике, металлургии, атомной, химической и других отраслях. Большая ответственность при этом ложится на персонал. Основное число крупных аварий и катастроф последнего времени связано с человеческим фактором. Доменное производство относится к числу потенциально опасных и возможные здесь аварии могут привести к значительным социальным и экономическим проблемам. Необходимость повышения его эффективности дополнительно накладывает высокие требования к действиям персонала. Применение современных методов и средств контроля и управления доменным процессом в этой связи трудно переоценить.

В идеальном случае исключение человека из управленческого цикла возможно посредством полной автоматизации управления работой доменной печи. Однако такая система пока не реализована из-за объективных препятствий:

• сложность процессов, происходящих в печи, и связанные с этим проблемы разработки математических моделей, достаточно точных и адекватных в любой ситуации;

• необходимость принятия решений и их реализация в ограниченный промежуток времени;

• изменение обязанностей персонала, необходимость повышения квалификации;

• сложность гарантирования оптимальности принимаемых решений из-за большого количества критериев и ограничений.

Выход из положения — разработать на основе существующих моделей, описывающих основные процессы в доменной печи, процедуру, которая в необходимые моменты времени дает рекомендации человеку, отвечающему за течение и результат процесса (в данном случае мастеру доменной печи), о выборе тех или иных управляющих воздействий. Окончательное решение остается за мастером. Эта

Сучков Андрей Владимирович — УГТУ-УПИ им. первого Президента России Б.Н. Ельцина, аспирант,

E-mail: a suchkov@list.ru

процедура, реализованная с использованием компьютерной техники, получила название система поддержки принятия решений (СППР).

СППР — это интерактивные

автоматизированные системы, помогающие лицу, принимающему решения (ЛИР), использовать данные и модели для решения слабоструктурированных проблем. Описание предлагаемой СППР является предметом настоящей статьи.

Общая постановка задачи и подход к ее решению.

Доменное производство является сложным, контроль за процессом и управление им требует учета большого числа параметров. Из них необходимо выделить входные и выходные

параметры. К первым относятся физические характеристики печи, характеристики шихты,

параметры дутья, ко вторым — производительность печи, температура и состав полученного чугуна, шлака, колошникового газа.

С точки зрения управления необходимо

определить управляемые и неуправляемые переменные, целевые критерии и ограничения. К числу управляемых переменных относятся

некоторые характеристики шихты (например, соотношение рудных материалов), основные

параметры дутья, выходные параметры печи. Неуправляемые параметры — это физические параметры печи, часть характеристик шихты, погодные условия.

В качестве целевых выбираются те критерии, которые нужно минимизировать или максимизировать (в зависимости от условий задачи). К ним, например, может относиться удельный расход кокса, производительность печи, экономические критерии. На остальные переменные накладываются ограничения, либо односторонние, либо двусторонние. Некоторые их них являются объективными, например, связанные с

возможностями оборудования, другие —

субъективными, зависящими от поставленных целей. Иногда переменные могут задаваться точечными оценками.

Модель управления доменным процессом, которую можно отождествить с СППР, к настоящему времени не разработана. Однако для решения данной проблемы можно применить

описательные модели доменного процесса. Тогда процесс определения значений необходимых

управляющих воздействий будет заключаться в последовательном применении модели печи с варьированием выбранных переменных для оценки выходных параметров печи и целевого критерия. Должны быть найдены все наборы этих воздействий для получения значений целевого критерия, близких к наилучшему при соблюдении ограничений,

налагаемых на остальные выходные параметры.

Предлагаемая процедура выработки

рекомендаций по управлению доменным

Выбор управляющих воздействий

осуществляется на основе циклической процедуры использования модели доменного процесса, идентифицированной в соответствии с конкретным производством. Однако при ее реализации

необходимо решить несколько проблем,

возникающих на определенных этапах. Перейдем к рассмотрению этапов процедуры выработки

рекомендаций по управлению доменной печью.

1. Выбор модели доменного процесса, адаптация к реальному объекту. Ее программная реализация (если отсутствует) и модификация (при необходимости).

2. Формирование целевого критерия модели управления.

3. Определение выходных переменных модели

управления, их желаемых значений,

4. Определение набора управляющих воздействий для данной ситуации и пределов их варьирования.

5. Выбор шага изменения значений для каждого из управляющих воздействий.

6. Нахождение подходящих наборов значений управляющих воздействий.

7. Сокращение найденного на этапе 6 множества решений.

8. Формирование рекомендаций, в случае если на этапе 6 не найдены решения.

9. Доведение полученной информации до лица, принимающего решения.

Рассмотрим проблемы, возникающие на каждом этапе, и возможные пути их решения.

Этап 1. Математические модели доменного производства создаются на основе разных подходов и для разных целей, количество существующих моделей достаточно велико.

На основании технологической инструкции, опыта работы и данных математического моделирования формируется так называемая стратегическая логическая поведенческая модель печи в виде определенного множества пар «состояние-управление» доменной печи, при этом «состояние» определяется выходными параметрами, а «управление» — управляющими воздействиями и, в

частности, отклонениями выходных параметров и управляющих воздействий от состояния «норма».

Используя указанное множество пар, логическое вычислительное устройство,

построенное в виде таблиц или композиции блоков, устанавливает качественные зависимости между выходными параметрами и управляющими воздействиями печи в виде знака при отклонении от нормы выходного параметра («больше» или «меньше») для того или иного управляющего воздействия.

Советчик (СППР) на основе такой модели существует [1], но его недостатком для практического использования является отсутствие числовых вычислений и рекомендаций.

Модели, построенные по принципу черного ящика.

Сущность этого метода создания модели заключается в том, что вся область используемых значений входов и выходов объекта моделирования исследуется экспериментально и на основе данных эксперимента устанавливаются математические соотношения между входами и выходами [2].

В качестве его главных достоинств выделяют простоту, разработанность и предопределенность применяемого математического аппарата. Недостатки этого подхода к моделированию очевидны. Метод «черного ящика» характеризуется недостаточной информативностью,

ограниченностью областью результатов,

подвергнутой экспериментальному обследованию. Полученные модели не вскрывают истинных причин явлений, происходящих в доменном процессе. Полученные количественные зависимости между параметрами и показателями процесса справедливы только для доменных печей, на которых они были установлены. Это является характерной особенностью всех моделей данного типа, не позволяющей использовать их для разработки обобщенной методики анализа работы доменных печей.

При данном подходе модель строится, исходя из внутренней структуры явлений, протекающих в системе. В этом случае входные и выходные параметры модели связываются друг с другом на основании универсальных законов сохранения и других фундаментальных физических и физикохимических закономерностей [2]. Полученное математическое описание процесса имеет более высокую информативность, широкую область применения, универсальность.

В зависимости от степени детализации явлений при аналитическом описании процесса различают балансовые и кинетические модели доменного процесса. Балансовые модели доменного процесса описывают закономерности тепломассообмена в самом общем виде. В основе их лежат материальные и тепловые балансы, устанавливающие взаимосвязи между режимными параметрами процесса,

показателями работы печи и показателями ее теплового состояния. Такая модель может включать зональные тепловые балансы, тогда имеется возможность определить характер распределения тепла по высоте печи, рассчитать температуру колошникового газа. Составление и решение системы дифференциальных уравнений,

описывающих закономерности тепло- и массообмена с учетом кинетики протекающих в объеме печи химических реакций, лежит в основе так называемых кинетических моделей доменного процесса.

В Институте металлургии УрО РАН разработана балансовая логико-статистическая модель [3]. Она включает в себя балансовую модель, наиболее значимые с точки зрения конечных результатов закономерности тепло- и массообмена, статистические данные. В качестве исходных данных используются только независимые переменные, в том числе такие характеристики материалов, как холодная и горячая прочность, восстановимость, гранулометрический состав и др.; внутренние параметры, в частности степень использования восстановительного потенциала горнового газа и температура колошникового газа как результаты расчета. Это обеспечивает возможность решения задач по оптимизации свойств сырья и параметров плавки, включая расходы кислорода и углеводородной добавки с учетом их ресурсов и взаимовлияния. Выходным параметром наряду с другими является производительность печи (за счет введения логикостатистического блока).

Разработанная в УГТУ-УПИ в рамках натурномодельного подхода балансовая модель доменного процесса в общем виде представляет собой систему детерминированных зависимостей,

характеризующих тепловой, восстановительный и газодинамический режимы доменной плавки [2]. Принятая при описании концепция опорновозмущенного движения позволяет решать как задачи статики, так и задачи динамики с применением относительно простого

математического аппарата, но базирующиеся на использовании физической сущности процессов, протекающих в доменной печи.

Условно модель УГТУ можно разделить на 2 части — модель базового состояния и прогнозирующую модель. Модель базового (эталонного) состояния позволяет ретроспективно оценивать состояние процесса по усредненным показателям за базовый (эталонный) период работы печи. При этом используется вся фактически доступная информация о параметрах шихты, комбинированного дутья, колошникового газа и продуктов плавки. Прогнозирующая же модель на основании результатов, полученных с помощью модели базового состояния, позволяет оценить показатели доменного процесса в случае изменения условий плавки.

При модельной поддержке принятия решений выделим следующие основные подсистемы:

• теплового состояния доменной печи;

• дутьевого и газодинамического режимов доменной плавки;

Пакет прикладных программ, реализующих данную модель, позволяет решать следующие технологические задачи:

• расчет показателей, характеризующих основные процессы доменной плавки, для анализа работы печи за рассматриваемый период;

• анализ причин изменения показателей работы

доменной печи за два сопоставимых периода. Здесь дается расшифровка причин изменения удельного расхода кокса. При решении задачи дополнительно рассчитываются: размер

фурменного очага, газодинамические характеристики слоя шихтовых материалов, характеристики свойств шлака, а также выполняется расчет материального и теплового балансов доменной плавки;

• расчет требуемого изменения расхода кокса и

флюсов при изменении соотношения расходных материалов или замене одного вида сырья на другой. Здесь учитывается изменение не только химического, но и гранулометрического состава железорудного материала и кокса. Определяется ожидаемое (с учетом сохранения перепада давления) изменение производительности печи и

• расчет требуемого изменения расхода кокса и флюсов в подаче при заданном изменении состава чугуна и шлака.

Кроме балансовых существуют

математические модели, описывающие отдельные явления доменной плавки: газодинамики, движения шихты, тепло- и массообмена и др.

Одной из основных проблем моделей

газодинамики в доменной печи является задание или расчет характера изменения сопротивления газовому потоку (перепада давления) по высоте слоя кусковых материалов. В настоящее время для этих целей широко применяется уравнение С. Эргана [4]:

ЗРр _ 150(1 — —) ‘иг +175———— ^Г ’ иГ (1)

dh еъ (Ф- dШ)3 ’ еъ Ф- dШ

где dш — диаметр куска шихты; — —

порозность (относительный объем пустот в слое); /ИГ — динамическая вязкость газа; иГ — условная

средняя скорость газа (в пустой шахте); СГ —

удельный расход газа; Ф — фактор (коэффициент)

формы (Ф равен 1,0 для шаров; 0,6-1,0 — для тел

Теоретически и экспериментально установлено, что эта формула достаточно адекватно

отражает характер изменения сопротивления газовому потоку по высоте слоя шихты.

В Московском институте стали и сплавов (МИСиС) разработан комплекс математических моделей доменного процесса и комплекс программ для ЭВМ в целях анализа работы доменных печей и разработки новых режимов плавки [4]. Комплекс состоит из моделей восстановления, газодинамики и теплообмена.

Восстановление оксидов железа описывается системой дифференциальных уравнений. Начальные условия определяются на основе анализа состава колошникового газа по радиусу, состава компонентов шихты, а также с помощью математической модели А. Риста, используемой для определения соотношения прямого и косвенного восстановления. Температура шихты берется из уравнения теплообмена. Выходными параметрами модели восстановления являются нижняя граница зоны плавления, поля распределения степеней восстановления шихтовых материалов и окисленности газа-восстановителя.

В основу математической модели газодинамики положена краевая задача с использованием дифференциальных уравнений в частных производных. Падение давления описывается уравнением С. Эргана (1). Выходными параметрами модели газодинамики являются поля распределения давлений газа и его массовых скоростей. Предусмотрена возможность

определения более частой сетки в зоне плавления.

Выходными параметрами в модели теплообмена являются поля температур материала и газа в пространстве доменной печи. Задачи газодинамики и теплообмена решаются как

осесимметричные методом конечных элементов. С помощью комплекса моделей исследовался режим работы при использовании мелкодисперсных

коксовых заменителей (коксика, коксовых брикетов, угля) в количестве 10 % в смеси с агломератом.

Во ВНИИМТ разработана кинетическая модель доменного процесса [5]. Она включает в себя уравнения материального и теплового баланса, теплообмена между потоками газов и шихтовых материалов, кинетики основных физико-химических процессов, граничных условий, отражающих

технологические особенности доменного процесса. Впоследствии эта модель была дополнена

уравнениями динамики и описана как кинетикодинамическая.

Адекватность модели проверена на решении ряда задач: при использовании комбинированного дутья высоких параметров, металлизованных окатышей, горячих восстановительных газов.

Определен ряд динамических характеристик

доменных печей по различным каналам управления. Впоследствии эта модель была привлечена для исследования влияния физико-химических свойств шихты на показатели работы доменной печи.

В Институте металлургии УрО РАН создан комплекс двумерных математических моделей [4]. Физическая формулировка задачи заключается в следующем. В шахтной печи заданного профиля непрерывным потоком вдоль линий тока движутся навстречу друг другу газ и шихта с заданными начальными температурами. Фурменный очаг служит точечным источником газа и стоком материала, а поля скоростей шихты и газа подобны. Теплоемкость потока газа, суммарный коэффициент массообмена и суммарный коэффициент теплоотдачи являются функциями координаты, т.е. скорости газа в данной точке. Температуры начала размягчения и плавления, кроме химического и минералогического состава, являются еще и функцией степени восстановления.

Такая формулировка задачи позволяет ограничиться следующими математическими моделями: балансовой (равновесной) и двумерной, состоящей из моделей газодинамики, теплообмена, восстановления, зоны когезии.

Балансовая (равновесная) математическая модель. В основе математической модели лежат следующие предпосылки. Теплообмен в доменной печи завершен, т.е. на определенной части высоты существует малый перепад температур между газом и шихтой. В определенной зоне печи на стадии восстановления магнетита (Бе304) реакция восстановления вюстита (БеО) стремится к термодинамическому равновесию. Решаются системы уравнений для нижней зоны (1>700°С), состоящие из условия термодинамического равновесия, материального баланса углерода и теплового баланса, дополненные тепловым балансом верхней зоны (К700°С). Результатами расчета являются показатели доменной плавки, характеристики колошникового газа, тепловой баланс нижней зоны, тепловой баланс верхней зоны. Определенные таким образом показатели являются предельно достижимыми (минимальными) при данных параметрах шихты и дутья. Задание фактических степеней использования СО и Н2 позволяет определить фактические показатели доменной плавки. Балансовая модель может использоваться как самостоятельно, так и в комплексе двумерных моделей.

Математическая модель газодинамики. Распределение скоростей в плоскости, проходящей через ось фурмы и ось печи, будет описываться системой дифференциальных уравнений с частными производными, решая которую, получим формулы для расчета скорости газа в любой точке объема доменной печи. Результатами расчета являются выводимые на экран дисплея изображения газодинамической сетки движения, которая является неравномерной, и поля скоростей газа, т.е. значения скоростей в узлах сетки, на основании которой строятся линии равных скоростей.

Математическая модель теплообмена. В основу математической модели теплообмена доменной плавки положена известная задача о нагреве слоя при противоточном движении газа и

шихты. Приняты граничные условия, отражающие завершенность теплообмена и деление рабочего пространства печи на две зоны. Аналитическим путем получены формулы для расчета температур газа и шихты в любой точке печи. Результатом расчета являются выводимые на дисплей изотермы (линии равных температур) шихты и газа, а также распределения температур шихты и газа в любом горизонтальном или вертикальном сечении, используемые при адаптации модели и для анализа явлений.

Математическая модель восстановления. В основу математической модели восстановления оксидов железа положена система дифференциальных уравнений массообмена и восстановления. Результатом расчета являются поля степеней восстановления железа и концентрационных потенциалов газа.

Математическая модель зоны когезии. Расчетная форма зоны когезии, ее толщина и положение по высоте печи определяются характером неравномерности температерного поля и температурами размягчения и плавления железорудного материала. Результатом расчета является информация о размерах и форме зоны когезии, которая может быть представлена графически.

В Австралии центральной исследовательской лабораторией фирмы «Broken Hill Proprietary» (BHP) разработана математическая модель, имеющая следующие особенности [4]. Поток твердого материала вычисляется с использованием теории потенциального потока, потоки кокса и руды решаются отдельно. Принимается, что поток газа сжимаем, плотность изменяется как функция температуры, давления и состава газа. Потери давления и соответствующие векторы скорости газа определяются с помощью известного уравнения С. Эргана (1). Теплообмен вычисляется с использованием уравнения В. Ранца с эмпирическими модификациями. Скорости газа вычисляются согласно локальным скоростям химических реакций, взятым из литературы. Принято, что железорудная шихта размягчается при 1200 °С и плавится при 1400 °С. Использовались данные о распределении материалов, полученные с применением модели RABIT, модернизированной фирмой BHP, и данные о тепловых и материальных балансах модели BHP. С помощью этой модели был исследован длительный период работы доменной печи №5 в Port Kembla. В частности, были изучены причины образования настылей, а также рассчитаны распределения температур материалов для 10 вариантов распределений шихты.

Наиболее полной и доведенной до практического использования является двумерная математическая модель фирмы «Nippon Steel», получившая название BRIGHT [6]. Она состоит из шести подмоделей: распределения шихты, потока

газа, потока материала, химических реакций, потока расплава, теплообмена.

В модели газового потока уравнение С. Эргана (1) относительно перепада давления в плотном слое расширено до двумерной формы как уравнение движения и объединено с уравнением неразрывности, которое удовлетворяет

материальному балансу газа. Поток газа в доменной печи определяется решением этой комбинации уравнений. Распределение давления в печи устанавливается распространением двумерного уравнения С. Эргана на уравнение Лапласа.

Отмечено, что движение шихты в доменной печи теоретически до сих пор не прояснено. На основании анализа результатов разборки охлажденных доменных печей и экспериментов на физических моделях сделано предположение, что поведение опускающихся частиц подобно потенциальному потоку. В уравнение неразрывности вводится величина, учитывающая убыль объема шихты за счет горения и газификации кокса, усадки и плавления руды.

Расчеты по этим подмоделям проводятся в перечисленном выше порядке в цикле. Информация от датчиков как входная не используется, но модель имеет к ним доступ в целях ее адаптации или анализа явлений, имеющих место в доменной печи. Чем дальше в списке выполнения стоит подмодель, тем больше информации от предыдущих подмоделей она использует. О зоне когезии судят по усадке слоев руды. Усадка определяется по температуре шихты, которая вычисляется по степени восстановления и данным из подмодели теплообмена. В результате расчетов по модели BRIGHT определяются (в графическом виде): распределение шихты, линии тока газа и шихты, распределение степени восстановления,

распределение температур шихты и газа. Время расчета на компьютере FACOM M340 составляет 65 мин. Кроме определения зоны когезии модель BRIGHT использовалась для анализа влияния производительности печи и восстановимости агломерата на процессы доменной плавки. Кроме разработки режимов работы доменной печи модель пригодна для анализа новых процессов и влияния таких изменений параметров, которые нельзя исследовать на действующей доменной печи.

При выборе конкретной модели для создания системы поддержки принятия решений необходимо учитывать:

• тип данных, с которым работает модель (логическая, количественная);

• способ построения модели (подход черного ящика, балансовая, кинетическая);

• полнота модели (учет пространственного распределения и динамики процессов, химических реакций, движения газов и шихты и др.);

• адекватность и точность модели;

• доступность модели, в том числе ее программной реализации;

• сложность адаптации и настройки модели;

• время однократного расчета по программе модели.

Модель для создания системы поддержки принятия решений должна быть количественной, при этом, если она построена по принципу черного ящика, то неизбежны многочисленные ограничения. Поэтому предпочтительней использовать модели, созданные на основе аналитического подхода. Кинетические модели являются более полными, но отличаются низким быстродействием из-за наличия сложных систем уравнений. Сложность модели и время расчетов определяются, прежде всего,

используемым математическим аппаратом.

Конечные алгебраические или

трансцендентные уравнения применяют для

построения статических моделей, обыкновенные дифференциальные уравнения — для создания

динамических моделей объектов с

сосредоточенными переменными или статических моделей объектов с распределенными переменными, зависящими только от одной пространственной координаты. Дифференциальные уравнения в частных производных используют для математического описания динамики объектов с распределенными переменными и стационарных режимов тех же объектов, но с распределенностью более чем по одной пространственной координате.

Кроме того, сложность кинетических моделей, наличие эмпирических данных и различных коэффициентов делает их использование для стороннего человека затруднительным. Авторы [4] приводят высказывание А.Б. Шура и Ю.А. Шура, что кинетико-математическими моделями могут пользоваться лишь их разработчики и подтверждают справедливость этого высказывания на начало XXI века.

С учетом сказанного наиболее целесообразно в качестве основы СППР использовать балансовые модели.

Любая математическая модель доменной печи несовершенна, поэтому может быть модифицирована для лучшего соответствия выдвигаемым требованиям. Принято считать, что полное математическое описание доменного процесса должно включать в себя следующие модели [4]:

• распределения материалов на колошнике (загрузки);

• движения газа (газового потока);

• движения шихты (потока материала);

• фильтрации расплава (потока расплава);

• химических реакций (термодинамики и кинетики);

• размягчения — плавления шихты;

• балансовую (на основе общего или зональных тепловых балансов).

Известно множество математических моделей по каждому пункту и в комбинации по ряду из них. При этом общая модель может состоять из суммы подмоделей или являться решением общей системы уравнений. Таким образом, модификация может заключаться в добавлении отсутствующей подмодели либо в уточнении существующих. При этом необходимо анализировать целесообразность такой модернизации и учитывать быстродействие модели.

Адаптация математических моделей осуществляется при помощи задания коэффициентов адаптации, получаемых на основе соответствия фактических и расчетных показателей плавки, параметров состояния. Этот процесс может быть разным по сложности и продолжительности для разных моделей, так как зависит от типа и полноты модели и многих особенностей ее реализации.

Этап 2. На этом этапе определяется целевой критерий, выбор которого зависит от сути проблемы. Обычно в качестве функции цели выбирается критерий, минимизирующий затраты или максимизирующий эффективность. В качестве примера в первом случае может быть удельный расход энергоносителя, во втором — объем производства, его рентабельность, уровень качества металла и другие. Предлагается ограничиться одним целевым критерием для упрощения задачи.

При решении поставленной задачи необходимо обеспечить лучшее значение критерия качества и, по возможности, относительное разнообразие наборов рекомендуемых значений управляющих воздействий, чтобы ЛПР мог выбрать наиболее предпочтительный исходя из неучитываемых и трудноформализуемых факторов, в том числе субъективных. При этом относительно малое отличие значения критерия качества от наилучшего, получаемое при некотором наборе управляющих параметров не является критичным, поскольку не может сильно влиять на показатели работы печи. Поэтому предлагается задание величины такой, что значения критерия качества, удаленные от оптимального менее чем на эту величину, считаются решением задачи. Это позволит существенно увеличить разнообразие наборов входных параметров, позволяющих достичь заданных результатов.

Этап 3. Необходимо определить выходные параметры. Выбираются характеристики, которые, как правило, не могут быть изменены напрямую, но являются важными и должны соответствовать заданному уровню. Для доменного производства в качестве выходных могут быть выбраны удельный расход кокса, теоретическая температура горения, производительность печи, условия, параметры, характеризующие состав чугуна и шлака. Для каждого из выбранных выходных параметров необходимо задать допустимую погрешность (можно это интерпретировать как допустимый

интервал). Значение и погрешность задаются исходя из требований: обеспечения нормального

протекание процесса (например, теоретическая температура горения), достижения определенного уровня качества продукции (содержание кремния в чугуне), обеспечения лучшего значения критерия качества процесса (минимизация расхода кокса).

Этап 4. В качестве управляющих выбираются параметры доменного процесса, которые оказывают влияние на ход процесса и показатели доменной плавки, при этом могут регулироваться человеком. В общем случае управляющими параметрами являются: соотношение железорудных частей

шихты (или содержание железа в шихте), объем подаваемого в печь природного газа, количество, температура и влажность дутья, содержание кислорода в дутье. При этом входные параметры модели управления не обязательно должны быть входными для доменного процесса; в качестве управляющей величины модели управления может рассматриваться заданная основность шлака. Входные же величины доменного процесса, такие как расход кокса и расход дутья, могут рассматриваться как выходные параметры модели управления и целевые критерии системы поддержки принятия решений.

В процессе работы пользователь должен выбрать пределы изменения управляющих параметров. Их определяют исходя из объективных технических и экономических требований или опыта лица, принимающего решения. В последнем случае, очевидно, технические ограничения должны соблюдаться. Можно выделить общие ограничения, присутствующие на сегодняшний день в доменном производстве [4,7].

Минимальная температура дутья может составлять около 800 — 900 °С, максимальная около 1200 — 1300 °С. Температуру дутья стремятся поднимать и далее, так как экономически оптимальные значения еще не достигнуты, но это требует совершенствования воздухонагревателей. Влажность дутья может изменяться от 3 г/м3 до 40 г/м3, при этом нижняя граница соответствует минимальной естественной влажности воздуха (зависит от климата), слишком же высокая влажность способствует снижению температуры горна. Содержание кислорода в дутье может меняться от 21% (при отсутствии обогащения дутья кислородом) до 30% и выше (в сочетании с вдуванием углеводородов). При этом ограничивающими факторами являются снижение температуры верха печи и перегрев горна, а также снижение перепада давлений по высоте печи. Расход природного газа может меняться от 0 до —130 м3/т чугуна. Большое количество вдуваемого природного газа влечет за собой охлаждение горна и увеличение перепада давлений по высоте печи. Совместное использование кислорода и природного газа, таким образом, позволяет скомпенсировать негативные эффекты от их применения. На отдельных предприятиях указанные верхние

пределы могут быть ниже из-за ограничений оборудования.

Содержание железа в шихте может изменяться примерно от 50% до 65%; при слишком низком содержании железа доменная плавка становится неэффективной (большой расход кокса и выход шлака), обогащение же шихты выше указанного предела экономически невыгодно.

Основность шлаков находится в диапазоне 0,8 — 1,3. Слишком низкие значения не позволяют эффективно удалять серу из чугуна, а высокие способствуют слишком резкому загустеванию шлака, что может нарушить ровный ход печи.

Учитывая объективные ограничения, ЛПР может задать более узкий диапазон, чем это позволяют технические и экономические условия, исходя из собственного опыта и текущих условий плавки. Это может исключить из рассмотрения достижимые, но нежелательные в данных условиях значения управляющих параметров.

Этап 5. Необходимо выбрать шаг изменения входных воздействий. Это связано с тем обстоятельством, что входные воздействия являются непрерывными. Однако имеется необходимость оперировать с ними, как с дискретными величинами. Это продиктовано, с одной стороны, технологическими требованиями (так как на практике управляющая величина может меняться дискретно с определенным шагом, обусловленным возможностями оборудования), с другой стороны, использованием для целей моделирования цифровых вычислительных машин. При выборе шага можно использовать, например, теорему Котельникова [8] — для возможности восстановления непрерывной функции; либо

руководствоваться опытом и технологическими

особенностями оборудования. Слишком малая

величина шага может чрезмерно увеличить объем вычислений, слишком большая — снизить точность и повысить вероятность потери значимых результатов.

Этап 6. Данный этап является ключевым, здесь происходит поиск нужных значений управляющих воздействий. Необходимо найти все сочетания управляющих параметров, при которых выполняются требуемые ограничения выходных характеристик печи (например, теоретическая температура горения в пределах 2000±50 °С) и показатель качества близок к оптимальному (например, удельный расход кокса, превышающий минимально достижимое значение не более, чем на 5 кг/т чугуна). Рассмотрим возможные варианты решения данной задачи.

Наборов входных параметров,

удовлетворяющих решению задачи, может быть достаточно много. Вид функции качества неизвестен, в общем случае она имеет много экстремумов. Описанные условия делают практически невозможным использование

статистических методов поиска (случайные

алгоритмы и детерминированные, за исключением метода сканирования) [9].

Можно рассмотреть использование парных зависимостей величин для целей регулирования. Для каждой входной величины находится ее влияние на каждую выходную и отображается в виде графиков или таблиц. Затем, по таблицам находятся значения необходимых выходных величин, в том числе минимальная величина критерия качества, и соответствующие им входные параметры. Так как каждая входная величина может влиять на несколько выходных, то процедура поиска по парным зависимостям должна быть итерационной. То обстоятельство, что входные величины также зависят друг от друга, значительно усложняет использование этого подхода. Рассмотрим повышение температуры дутья с 1000 °С до 1100 °С для печи объемом 1719 м3. Автором получено, что при содержании кислорода в дутье 21% и влаги 40 г/м3 такое изменение дает снижение расхода кокса на 16 кг/т чугуна. При содержании кислорода 25% и влаги 10 г/м3 это повышение температуры позволяет снизить расход кокса на 11 кг/т чугуна. Следовательно, степень влияния входного параметра на выходной может меняться. Использование парных зависимостей выходных параметров от входных возможно только при задании большого количества дополнительных условий, которые значительно усложняют задачу, могут отличаться для разных печей, а также приводят к увеличению погрешности вычислений. Для приведенного примера таким условием является учет значений содержания кислорода в дутье и влажности дутья. То есть необходимо найти некоторое количество зависимостей расхода кокса от температуры дутья, найденных при разных значениях упомянутых входных параметров.

Для решения поставленной задачи предлагается использовать метод сканирования (полного перебора). В этом случае осуществляется перебор всех сочетаний дискретных значений управляющих величин. Для каждого сочетания производится расчет выходных величин с помощью модели печи, в случае удовлетворения выходных параметров заданным ограничениям, сочетание входных воздействий считается возможным решением. Определяется оптимальное значение целевого критерия среди полученных наборов значений, отбираются только те из них, которые имеют критерий качества, близкий к оптимальному.

При этом количество расчетов по модели (итераций) составит:

Р1 — число шагов, на которые разбивается диапазон 1 входной величины

п — число управляющих величин

Число шагов Р1 для 1 входной величины рассчитывается так:

Р1 = Ш((Хшш — Хщач)^ )+1 (3)

Ш — целая часть дробного числа (операция округления дробного числа в меньшую сторону)

Х1нач — нижняя граница диапазона

Х1кон — верхняя граница диапазона

81 — величина шага

Этот метод требует большого количества вычислений. Для сокращения объема расчетов и, соответственно, времени поиска решений, можно использовать некоторые модификации.

Для упрощения описания действий, производимых со значениями параметров доменной печи, введем многомерное пространство, координатами которого являются управляющие

воздействия, единичным отрезком для каждого измерения является шаг изменения

соответствующего параметра. Точке в пространстве будет соответствовать набор управляющих

Все входные и выходные параметры

доменного процесса непрерывны. Ввиду значительной инерционности процесса и взаимосвязи параметров при малых изменениях входной величины, выходная меняется на еще меньшую относительную величину. Исходя из этого, можно сделать следующее предположение: если точке пространства параметров соответствуют выходные значения, находящиеся относительно далеко от границ требуемых диапазонов, то соседние точки пространства также не будут удовлетворять заданным условиям. Это предположение подтверждается на практике и позволяет, в ряде случаев, увеличить шаг поиска, то есть величины изменения значений входных параметров модели. Для большего удобства

последующей обработки результатов увеличенный шаг лучше принимать кратным исходному. Для принятия решения о том, что выходные значения, соответствующие точке пространства, значительно удалены от требуемых диапазонов, можно использовать заданную величину погрешности для

выходной величины (например, удаление

значительно, если расстояние больше, чем удвоенная погрешность). Такой анализ должен производиться на каждом шаге, но он относительно несложен, а итоговое время вычислений

Одной из причин большого объема вычислений при переборе значений входных величин может быть большое число управляющих параметров. Это, в свою очередь, затрудняет выбор и реализацию рекомендаций. Сложно также учитывать все переходные процессы, ведь влияние разных факторов на доменный процесс отличается по времени. Таким образом, представляется, что система должна давать совет с числом одновременно изменяемых параметров от 2 до 4. Число это может задаваться пользователем или быть установленным жестко при реализации программы. Если заданное число управляющих переменных больше, можно использовать часть параметров

(например, 3 из 6) для перебора и формирования рекомендаций, затем менять состав одновременно изменяемых параметров, в конечном итоге использовав все сочетания. Известно, что количество таких сочетаний равно:

Несмотря на большое число сочетаний, количество вычислений в таком случае меньше, чем при полном переборе.

Этап 7. На этом этапе происходит сокращение найденного множества решений для случая их большого количества. Если же решения не найдены, он пропускается.

Заданные выходные условия могут выполнятся при разных сочетаниях входных параметров. Шаг изменения входных величин в общем случае относительно небольшой, поэтому количество решений может быть значительным, доходя до нескольких сотен. Вывод такого числа рекомендаций неприемлем, поэтому необходимо сокращение их количества с максимальным сохранением разнообразия возможностей исходного количества вариантов. Для этого нужно оставить часть вариантов, которые могут быть охарактеризованы как ключевые, остальные -сократить.

Для решения этой задачи могут использоваться методы кластерного анализа [10,11]. Кластерный анализ — задача разбиения заданной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. После разбиения множества решений на кластеры нужно найти ключевые решения для каждого кластера, например, ближайшие к его центру, и в качестве итоговых оставить только их.

Для решения задачи кластеризации может использоваться один из известных методов, например, алгоритм БОИБЬ, метод к-средних, иерархические алгоритмы, в том числе агломеративные и дивизимные и другие. При их использовании, однако, возникают трудности. Они предназначены для разбиения множества точек, расположенных хаотично в многомерном пространстве. Широко используется вычисление расстояний, в том числе минимального расстояния между двумя точками, нахождение скоплений точек. При имеющемся равномерном дискретном распределении точек использование некоторых алгоритмов, например, иерархических, невозможно. Также существующие методы, в силу своей универсальности, сложны и требуют большого количества вычислений. Проблемой является выбор начальных центров кластеров в алгоритме БОИБЬ, задания числа кластеров в методе к-средних. При использовании известных методов кластеризации также не решается задача обеспечения заданной

точности сокращения, другими словами, размера кластера по всем измерениям.

В связи с трудностями использования существующих алгоритмов целесообразно использовать эвристический подход к разбиению множества решений. Он должен предусматривать, в общем случае, распределение дискретных результатов по областям, относительно удаленным друг от друга и последующее разделение этих областей на участки заданного размера для получения итоговых результатов. Также, нужно учесть, что в процессе управления часто наиболее предпочтительными являются крайние значения управляющих параметров, обеспечивающие нужные результаты, например, минимальное содержание железа в шихте (что позволяет использовать более дешевую руду).

Этап 8. На данном этапе рассматривается возможность формирования рекомендаций при отсутствии решений, например, по изменению заданных пользователем ограничений для входных и выходных параметров. Особенно актуально это в случае задания диапазонов для управляющих параметров более узкими, чем позволяют технические возможности и требования. Тогда в эвристическом алгоритме также методом перебора ищутся решения, но поочередно расширяется диапазон для каждого входного параметра. Шаг изменения для управляющих величин также может быть увеличен для сокращения времени расчетов. При нахождении решения поиск в данном диапазоне прекращается, и отличие входной величины в большую или меньшую сторону от исходного диапазона выдается в качестве совета после окончания процедуры поиска. Такая рекомендация, например, может выглядеть следующим образом: «Снизить минимальный заданный уровень расхода природного газа». Аналогично анализируются результаты при увеличении заданной погрешности поочередно для каждой выходной величины, и в случае нахождения результатов с новыми параметрами, направление изменения выходной величины выдается в качестве совета. Может проверяться также возможность получения решения при изменении входных величин, заданных пользователем однозначно.

Этап 9. На данном этапе происходит вывод результатов. Полученное множество решений выводится в виде сочетаний значений входных параметров и соответствующих им выходных. Удобнее всего эти наборы представить в виде таблицы, где строкам соответствуют разные решения, а столбцам входные (в левой части) и выходные (в правой части) параметры. Вывод может производиться в программе системы поддержки принятия решений или при помощи дополнительных программ, таких как MS Excel. Также, результаты и настройки могут быть сохранены в виде текстового или другого файла.

Если пользователь хочет изменить какие-либо начальные условия с целью получения других рекомендаций, он может это сделать после вывода результатов. После запуска процедура выработки рекомендаций выполнится еще раз, и будут получены новые значения управляющих воздействий.

В статье предложен подход к построению системы поддержки принятия решений в доменном производстве, в основе которого лежит математическая модель печи. Советчик,

работающий по описанным принципам, был установлен на компьютеры доменного цеха Чусовского металлургического завода для практического использования.

Описанные принципы построения СППР могут использоваться и для других производств и технологических процессов, для которых

существует соответствующая математическая

модель. При этом должен быть найден компромисс между простотой модели, чтобы время

формирования рекомендаций было приемлемым, и полнотой — для обеспечения ее адекватности.

С развитием микропроцессорной техники, в том числе многоядерных процессоров, ростом скорости вычислений, предложенный метод создания советчика (системы поддержки принятия решений) становится более актуальным, поскольку появляется возможность увеличить количество управляющих параметров, доступных для перебора, уменьшить шаг изменения входной величины (таким образом повысив точность), уменьшить время вычислений.

1. Чистов В.П. Разработка экспертной системы на основе логического интеллекта для управления доменной печью / В.П. Чистов, В.Г. Лисиенко, Л.И. Леонтьев [и др.]. Наука и инженерное творчество — XXI веку: Первая

научно-техническая конференция РУО АИН РФ. Екатеринбург: РУО АИН РФ, 1995. С. 89 — 92.

2. Информационные системы в металлургии: Учебник для вузов / Н.А. Спирин, Ю.В. Ипатов, В.И. Лобанов, В.А. Краснобаев, В.В. Лавров, В.Ю. Рыболовлев, В.С. Швыдкий, С.А. Загайнов, О.П. Онорин. Екатеринбург: Уральский государственный технический университет — УПИ, 2001. — 617 с.

3. Ченцов А.В., Чесноков Ю.А., Шаврин С.В. Балансовая логико-статистическая модель доменного процесса. — Екатеринбург: УрО РАН, 2003. — 164с.

4. А.Н. Дмитриев, Н.С. Шумаков, Л.И. Леонтьев, О.П. Онорин Основы теории и технологии доменной плавки. — Екатеринбург: УрО РАН, 2005, -548с.

5. Мойкин В.И., Боковиков Б.А., Бабушкин Н.М., Репин С.М. Определение динамических характеристик доменного процесса с помощью математической модели // Повышение производительности и экономичности работы тепловых металлургических агрегатов. М.: Металлургия, 1982. С. 42-46.

6. Development of mathematical model of blast furnace. Shinroku Matsuzaki, Akihiko Shinotake, Tsunehisa Nishimura. Nippon steel technical report No 94 yuly 2006.

7. Воскобойников В.Г., Кудрин В.А., Якушев А.М. Общая металлургия. — М.: Металлургия, 1998. — 768с.

8. Ричард Рид. Основы теории передачи информации. Изд-во «Вильямс», 2004 г., 304 с.

9. Растригин Л.А. Статистические методы поиска. Главная редакция физико-математической литературы изд.-ва «Наука», 1968, 376 с.

10. Гитис Х.Л. Кластерный анализ в задачах классификации, оптимизации и прогнозирования. Издательство Московского государственного горного университета, 2001, 104 с.

11. Дюран Б, Оделл П. Кластерный анализ. Пер. с англ. Е.З. Демиденко. Под ред. А.Я.Боярского. М., «Статистика», 1977, 128 с.

Уральский государственный технический университет — УПИ им. первого Президента России Б.Н. Ельцина

PROBLEMS OF CONSTRUCTING A DECISION SUPPORT SYSTEM FOR BLAST

Математическое моделирование сложных технологических процессов доменного производства методами нелинейной динамики тема диссертации и автореферата по ВАК РФ 05.13.18, кандидат технических наук Голубев, Олег Викторович

Оглавление диссертации кандидат технических наук Голубев, Олег Викторович

Глава 1. Доменный процесс выплавки чугуна и моделирование сложных термодинамических систем

Читайте также ПРОДУКТЫ ДОМЕННОЙ ПЛАВКИ

1.1. Краткое описание доменного процесса

1.2. Неравновесная термодинамика и методы нелинейной динамики

1.3. Численные методы решения дифференциальных уравнений

1.4. Исследование точности численного решения динамических систем

1.5. Иерархия упрощенных моделей 50 Выводы

Глава 2. Моделирование процессов нагрева и охлаждения насадки доменного воздухонагревателя

2.1. Воздухонагреватели. Типы и основные характеристики

2.2. Модель теплового состояния насадки воздухонагревателя

2.3. Физическая модель воздухонагревателя с учетом суперпозиции действующих сил

2.4. Компьютерное моделирование процесса нагрева и охлаждения насадки воздухонагревателя

2.5. Рассмотрение возможных способов нагрева и охлаждения насадки

2.6. Влияние шага дискретизации в математической модели насадки воздухонагревателя 82 Выводы

Глава 3. Моделирование процесса косвенного восстановления железа в доменной печи с использованием аппарата нелинейной динамики

3.1. Модель косвенного восстановления железа в доменной печи

Введение диссертации (часть автореферата) на тему «Математическое моделирование сложных технологических процессов доменного производства методами нелинейной динамики»

Изучение процессов, протекающих в системах реального мира, показывает, что поведение объектов зачастую носит сложный для его описания характер. Традиционные подходы к моделированию и исследованию динамики различного рода процессов, к которым относится и большинство процессов доменного производства чугуна, часто искажают картину истинного поведения объектов. Это обстоятельство ведет к снижению эффективности мероприятий, направленных на оптимизацию, автоматизацию и совершенствование процессов доменного производства.

Необходимость анализа металлургического производства вообще и объектов доменного производства, в частности, с позиций новой, активно разрабатываемой и развивающейся в последние десятилетия теории открытых дисси-пативных нелинейных систем, обусловлена практически полным отсутствием математических моделей этих процессов. В настоящее время, благодаря многочисленным работам таких крупных ученых, как лауреата Нобелевской премии И. Пригожина, Ю.Н. Неймарка, С.П. Курдюмова, Г.Г. Малинецкого и др., теория нелинейной динамики стала мощным инструментом, позволяющим описывать объекты, обладающие сложным поведением. Исследования объектов черной металлургии с использованием аппарата нелинейной динамики и неравновесной термодинамики активно развиваются, например, в научных школах В.П. Цымбала, Б.Н. Окорокова и др.

Еще одним затруднением при моделировании объектов доменного производства является то, что в них одновременно протекает большое число разнообразных физических и химических процессов. Кроме того, параметры, определяющие протекание данных процессов, трудноизмеримы, а набор управляющих воздействий, позволяющих проводить эксперименты на объекте, ограничен. При традиционном подходе единое описание поведения системы базируется на синтезе, основанном на анализе элементарных ситуаций и действующих в них законов. Использование этого подхода к сложным системам, в силу действия ряда причин (появление сложных движений, имеющих хаотический характер поведения, «проклятие размерности» для систем высокого порядка, отсутствие наглядности конечного результата, увеличение неустойчивости получаемого результата при повышении точности описания объекта и др.), приводит к тому, что становится невозможным получить свойства целого, изучая его части.

Перечисленные обстоятельства приводят к тому, что при моделировании процессов доменного производства необходимо, оставаясь в рамках теории нелинейной динамики, использовать подход, при котором построение модели основывается на бесспорных общепринятых непротиворечивых для специалистов положениях, с устранением из модели всех второстепенных процессов, ненаблюдаемых и неизмеримых параметров и переменных. Модели данного класса позволяют подтверждать и объяснять наблюдаемые и открывать новые особенности протекания процессов доменного производства, решать задачи оптимизации и автоматизации работы доменного производства.

Работа выполнялась в рамках разрабатываемого в ЛГТУ научного направления «Феноменологические модели и нелинейная динамика высокотемпературных процессов и технологий» при поддержке грантами Минобразования РФ ТОО — 5.2-2928 и ЛГТУ им. Коцаря С.Л. №0111.

Целью работы является повышение точности и минимизация вычислительных затрат при математическом моделировании сложных технологических процессов доменного производства выплавки чугуна на основе использования аппарата теории нелинейной динамики, а именно, процессов нагрева и охлаждения насадки доменного воздухонагревателя и косвенного восстановления железа в доменной печи. За счет применения математических моделей, основанных на аппарате нелинейных динамических систем, глубже понять процессы и явления, протекающие в агрегатах доменного производства выплавки чугуна, для их анализа, решения задач управления и оптимизации.

Исходя из цели работы, были определены следующие основные задачи исследования:

-проанализировать основные процессы доменного производства, определить особенности процессов, обусловленные нелинейными механизмами;

-вскрыть основные закономерности, лежащие в основе поведения моделируемых процессов, и на их базе разработать нелинейные математические модели;

— провести математическое исследование моделей и особенностей их численного решения. Для подтверждения адекватности модели реальному процессу сопоставить результаты моделирования с экспериментальными данными;

-разработать рекомендации по практическому применению результатов моделирования для управления процессами доменного производства.

Методы исследования. В работе использованы методы теории нелинейной динамики, неравновесной термодинамики, математического моделирования, теории автоматического управления, методы математического анализа, численные методы решения дифференциальных уравнений.

Научная новизна исследования. Разработаны математические модели процессов доменного производства (модель нагрева и охлаждения насадки доменного воздухонагревателя и модель косвенного восстановления железа доменной печи), общей особенностью которых является применение теории нелинейной динамики и неравновесной термодинамики к анализу процессов доменного производства. Использование разработанных моделей позволило математически описать процессы перераспределения потоков газов в насадке воздухонагревателя и впервые вскрыть наличие концентрационных колебаний реагентов в зоне косвенного восстановления железа доменной печи и, как следствие, выработать технологические рекомендации по их оптимизации.

Практическая значимость работы. Разработан комплекс прикладных программ, которые применимы в промышленных и учебных целях для решения задач моделирования, исследования и совершенствования доменного производства, а также решения проблемы их автоматизации и оптимизации. Программы «Моделирование процессов нагрева и охлаждения насадки воздухонагревателя доменной печи» и «Расчет корреляционной размерности для анализа временных рядов» зарегистрированы в Государственном фонде алгоритмов и программ Российской Федерации (№ 50200300116 от 26.02.2003 г. и № 50200300117 от 26.02.2003 г.). Созданные программные продукты могут быть использованы в качестве средств информационного обеспечения алгоритмов управления доменным процессом. Установлены режимы рационального функционирования процессов.

Внедрение результатов работы. Материалы диссертации включены в учебные курсы для инженеров и магистров металлургических специальностей ЛГТУ. Программные средства приняты ОАО «Липецкстальпроект» для использования в процессах моделирования процессов доменного производства.

Апробация работы. Основные положения диссертационной работы освещались на международной конференции «Asia Steel International Conference» (Beijing, 2000), международной научной конференции «Синергетика в современном мире» (Белгород, 2000), V международной электронной конференции «Современные проблемы информатизации в технике и технологиях» (Воронеж, 2000), IX областной научно-технической конференции «Повышение эффективности металлургического производства» (Липецк, 2000), международной научно-технической конференции «Теория и технология производства чугуна и стали» (Липецк, 2000), всероссийской научно-технической конференции «Современная металлургия начала нового тысячелетия» (Липецк, 2001), IX международной конференции «Математика. Компьютер. Образование» (Дубна, 2002).

Работа по исследованию влияния шага дискретизации на поведение динамических систем была удостоена премии имени С.Л. Коцаря областного Совета депутатов и администрации Липецкой области.

Публикации. Результаты исследований нашли свое отражение в 16 опубликованных в печати научных работах, в том числе двух программах, зарегистрированных в Государственном фонде алгоритмов и программ. Во всех работах личный вклад автора заключается в участии в постановке задач, разработке и анализе моделей, разработке алгоритмов, программировании задач и участии в вычислительном эксперименте.

Упрощенная модель доменной плавки

Доменная плавка относится к числу непрерывных металлургических процессов, в основу его механизма заложен принцип противотока, что обусловливает высокую экономичность протекающих при этом тепловых и массообменных процессов. Шихтовые материалы (в основном агломерат и кокс), загруженные на колошник доменной печи, медленно движутся вниз (время их пребывания в печи 6 – 12 ч), а им навстречу с довольно большой скоростью (время пребывания порядка нескольких секунд) поднимаются газы, образующиеся в результате сгорания кокса около дутьевых фурм. За это время газы отдают большую часть своего тепла шихтовым материалам и восстанавливают оксиды железа (косвенное восстановление) по схеме:

Восстановлению оксидов металла и снижению температуры плавления материалов способствует также непосредственный контакт кокса с агломератом, особенно по мере приближения к распару и заплечикам, где преобладающим являетсяпрямое восстановление:

Газопроницаемость материалов

Для равномерного распределения газового потока по сечению печи большое значение имеет газопроницаемость сырых материалов. Так как дутье поступает в печь в периферийной области, то газы, в первую очередь, стремятся подниматься вдоль стенок печи. Для выравнивания сопротивления газовому потоку стремятся загружать печь таким образом, чтобы у стен располагался более толстый слой агломерата, газосопротивление которого больше, чем кокса, а в центральной части находилось больше кокса.

Управляющие воздействия

Сверху

Распределение материалов по сечению является важнейшим управлением сверху, действующим, однако, с большим запаздыванием, сравнимым со временем пребывания шихты.

Снизу

Имеются также более быстродействующие управляющие воздействия, направленные снизу. К ним относятся: распределение дутья по фурмам, изменение влажности и температуры дутья, расхода интенсификаторов (кислорода, природного газа или мазута), подаваемых в доменную печь с целью развития процессов косвенного восстановления (в том числе за счет водорода), что приводит к повышению производительности печи и снижению расхода кокса.

Математическое построение модели (второй этап моделирования)

Этапы математического построения модели

Таким образом, даже из приведенной выше краткой характеристики можно видеть, что доменная плавка является очень сложным процессом, распределенным как в пространстве, так и во времени. Математическому описанию этого процесса посвящено большое количество работ. Из-за невозможности сколько-нибудь полного их обзора остановимся лишь на одном достаточно простом примере, удобном с точки зрения пояснения процесса создания модели.

Рассмотрим с этой целью разработанную на заводе Кокура (Япония) модель доменной плавки, предназначенную для использования в системе автоматического управления температурным режимом печи (температурой чугуна).

Прежде чем перейти к конкретным вопросам построения модели следует вспомнить (см. гл. 1), чтопроцесс моделирования состоит из ряда этапов. Первый из них (постановка задачи), связанный с анализом существующих представлений о процессе и учетом цели, кратко уже рассмотрен выше.

Второй этап состоит из двух ступеней: выбора структурной схемы модели и математического описания ее блоков.

Структурная схема модели

Упрощающие допущения

При разработке структурной схемы модели были приняты следующие упрощающие допущения:

распределение температуры и газового потока по сечению печи равномерное;
печь разделена на пять горизонтальных зон, в каждой из которых находятся определенные материалы и протекают соответствующие реакции;
сгорание топлива перед фурмами полное, а косвенное восстановление протекает стабильно;
находящиеся в каждой зоне материалы остаются неизменными;
учитываются только основные компоненты твердой и газообразной фазы;
в каждой зоне для твердой и газообразной фазы учитываются только средние температуры.

Структура модели

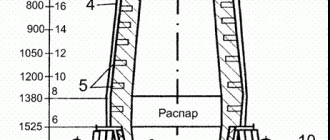
Упрощенно структура модели представлена на рис. 8.2.

Рис. 8.2 К построению модели теплового состояния доменной плавки

Здесь и в приводимых ниже формулах приняты следующие условные обозначения:

– температуры шихты по зонам;

– температуры газа по зонам;

, – средние удельные теплоемкости шихты и газа;

, – находящиеся в зоне количества шихты и газа;

, – скорости схода шихты и газового потока;

– количество тепла, получаемого газом в результате реакции ;

– коэффициент теплопередачи между газообразной и твердой фазами;

– адаптивные коэффициенты теплопередачи;

– индекс скорости реакции в зоне (если в зоне протекает реакция , то =1, если не протекает, то =0);

– содержание водорода в мазуте;

– температуры дутья и чугуна;

– степень использования водорода.

Математическое описание блоков модели

Задача создания комбинированной модели

На этапе математического описания ставится задача создания комбинированной (детерминированно-вероятностной) модели. Первая часть ее основана на законах сохранения вещества и энергии, рассмотренных в гл. 3. Вторая – на экспериментально – статистических методах (см. гл. 5).

Составление материального баланса

Определение скоростей реакций

Составление материального баланса начинается с определения скоростей реакций. Скорость каждой реакции косвенного восстановления () выводится из баланса кислорода с учетом допущения 3. Скорость восстановления водородом ( ) и расходование углерода ( ,) можно вывести соответственно из баланса водорода и углерода, при этом принимается, что . С учетом допущения 3 скорости реакций при сгорании топлива перед фурмами определяются непосредственно по параметрам дутья. В результате получена системауравнений скоростей реакций

По этим уравнениям можно рассчитать скорости реакций и в соответствии с составом колошникового газа.

Учитывая допущение 4, при определении скорости схода шихты и скорости газового потока принимают, что количество шихты и газа на выходе из зоны равно их количеству на входе в зону плюс продукты реакции, т. е.

Тепловой баланс

Изменение энтальпии в каждой зоне обусловлено нарушением теплового баланса; разницей между количествами тепла на входе и выходе зоны, теплот реакций, теплообмена между твердой и газообразной фазами, а также потерь тепла.

В связи с этим уравнения теплового баланса для твердой и газообразной фаз в каждой зоне можно записать следующим образом:

(8.6) При расчете теплового баланса для газообразной фазы коэффициент теплопередачи рассчитывался по эмпирической формуле. Эти взаимосвязи можно представить дифференциальным уравнением следующего вида:

Так как при стационарном состоянии печи , то температуры твердой и газообразной фаз в каждой зоне можно рассчитать по измеряемым параметрам с использованием получаемого в этом случае соотношения . Адаптивные параметры теплопередачи и выбираются при этом с помощью итеративной процедуры таким образом, чтобы расчетные температуры и совпадали с фактической температурой колошникового газа и жидкого чугуна. Далее в процессе экспериментальной проверки и использования модели подстраиваются по информации об обратной связи еще несколько параметров, учитывающих, в частности, конкретные условия протекания реакций и и степень использования, например, водорода . Для этого применяются алгоритмы, близкие по смыслу к адаптивным шаговым методам, рассмотренным в гл. 5, например, вида:

– число циклов адаптации или управления;

– подстроечный параметр алгоритма адаптации.

Использование модели

Проблемы

Для возможности использования рассмотренной выше модели [уравнения (8.3 – 8.8)] в качестве прогнозирующей в системе управления температурой чугуна необходимо знать динамические характеристики процесса по каналам управляющих воздействий: расходам мазута и кокса, влажности и температуре дутья.

Решения

Эта задача может быть сведена к экспериментальному определению зависимостей во времени от упомянутых входных факторов (временных характеристик) скоростей реакций и температуры чугуна. С использованием методики, аналогичной описанной в §3 гл. 5, эти характеристики аппроксимируются апериодическим звеном первого порядка и чистым запаздыванием и представляются в виде весовой (импульсной) функции следующим образом:

– численные значения постоянной времени;

– коэффициент передачи объекта;

– время чистого запаздывания.

Прогнозирующая модель

В результате для прогнозирующей модели уравнения скоростей реакций и в системе (8.3) принимают вид:

– скорость реакции в момент ;

– адаптивный член обратной связи, рассчитываемый по соотношению .

Полученная выше прогнозирующая адаптивная модель [уравнения вида 8.3 – 8.9 с уточнениями типа (8.10)] составляет основу алгоритма системы управления температурой чугуна. Коротко принцип ее работы близок к рассмотренному на рис. 6.5 и 6.6. Cпрогнозированное с помощью модели значение температуры чугуна с определенным интервалом опережения (например 12 ч) сравнивается с заданным для этого же момента времени. В случае их расхождения путем эксперимента на модели заранее выбираются значения управляющих воздействий, обеспечивающие выполнение задания на прогнозируемый момент времени. Обратная связь по отклонению прогнозируемых с помощью модели выходов от фактических используется для адаптации модели.

Исследование и экспериментальная проверка модели (этапы 3 и 4, см. §2 гл. 1) показали возможность прогнозирования температуры чугуна с точностью порядка , а построенная на основе этой модели система управления позволила существенно снизить расход топлива.

Источник https://cyberleninka.ru/article/n/problemy-postroeniya-sistemy-podderzhki-prinyatiya-resheniy-dlya-domennogo-proizvodstva

Источник https://www.dissercat.com/content/matematicheskoe-modelirovanie-slozhnykh-tekhnologicheskikh-protsessov-domennogo-proizvodstva

Источник https://bookaa.ru/matematicheskoe-modelirovanie/uproshhennaya-model-domennoy-plavki.html